Prime numbers are positive integers that can only be divided evenly by 1 or themselves. By definition, negative integers, 0, and 1 are not considered prime numbers. The list of the first few prime numbers looks like:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ...

For example, 5 is a prime number because you can divide 5 by 1 evenly and divide 5 by 5 without a remainder, but if you divide 5 by any other integer, you get a remainder.

5/1 = 5
5/2 = 2 plus a remainder
5/3 = 1 plus a remainder
5/4 = 1 plus a remainder
5/5 = 1
5/6 = 0 plus a remainder
... = 0 plus a remainder

Now look at the number 4 which is not a prime.

4/1 = 4
4/2 = 2
4/3 = 1 plus a remainder
4/4 = 1
4/5 = 0 plus a remainder
... = 0 plus a remainder

The number 4 can be divided by 2 evenly, so it is not a prime.

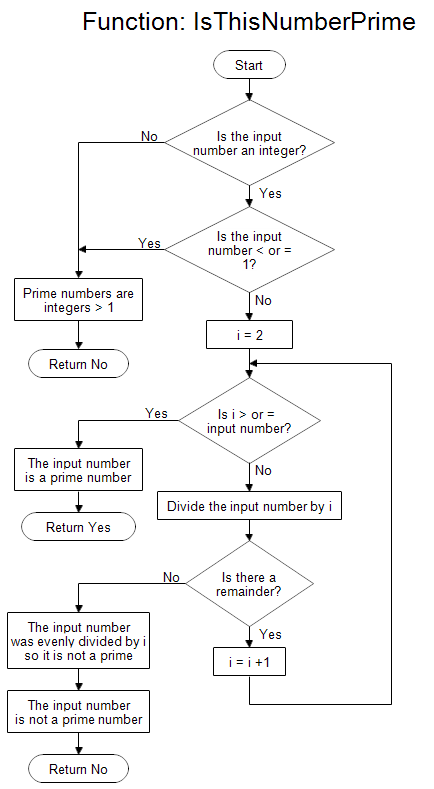
The flowchart shown above describes a function that is given a number i and returns whether it is prime or not. The name of the function is "IsThisNumberPrime." First it checks to make sure the input number is an integer. Then it checks to make sure the input number is not negative, 0 , or 1. Negative integers, 0, and 1 are not considered prime by definition.

Next the function tries to divide the input number by i, where i = 2, 3, 4, 5, and so forth, to see if it divides any of them evenly, that is, without a remainder. If the input number is divided evenly, it is not a prime. The check stops when i is equal to the input number.

You give the function a number and the output is "Yes" if the number is prime, or "No" if it is not.

Now suppose you want to calculate the first 100 prime numbers. A flowchart to show that process is shown below.
The flowchart above starts with the number 2 and checks each number 3, 4, 5, and so forth. Each time it finds a prime it prints the number and increments a counter. When the counter hits 100, it stops the process. To determine whether a number is prime, it calls the function "IsThisNumberPrime" which is shown at the top of this page.

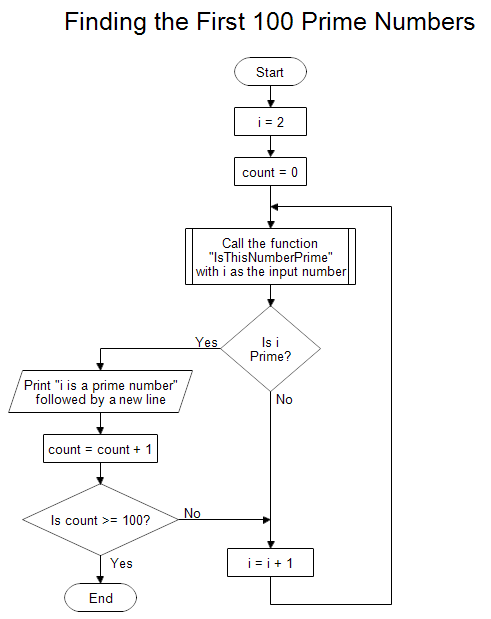
The first few primes are quickly calculated, but as the primes get further apart the computation time increases. Finding large primes is a task for super computers.

If you haven't already done so, first download the free trial version of RFFlow. It will allow you to open any chart and make modifications.

Once RFFlow is installed, you can open the above charts in RFFlow. Click on prime-numbers.flo for the top flow chart or finding-prime-numbers.flo for the bottom flow chart. From there you can zoom in, edit, and print these sample charts. It is often easier to modify an existing chart than to draw it from scratch.

To draw this flow chart without downloading it, run RFFlow, click on the More Shapes button , scroll and open the Flowcharting folder, click the Physical Flowcharting stencil and click the Add Stencil button.